光学中有关衍射的推论与计算

夫琅禾费衍射公式：

\boxed{U(x,y)=\frac{1}{j \lambda z}e^{jkz}e^{j\frac{k}{2z}(x^2+y^2)}\iint_\infty^\infty{U(x_0,y_0)e^{-j\frac{2\pi}{\lambda z}(xx_0,yy_0)}dx_0dy_0}} \boxed{U(x,y)=\frac{1}{j \lambda z}e^{jkz}e^{j\frac{k}{2z}(x^2+y^2)}[\mathscr{F}\{U(x_0,y_0)\}|_{f_x=\frac{x}{\lambda z}, f_y=\frac{y}{\lambda z}}]}

$f_x=\frac{x}{\lambda z}, f_y=\frac{y}{\lambda z}$

第13题，孔径函数：

$t(x_0,y_0)=comb(\frac{x_0}{a})comb(\frac{y_0}{a})+comb(\frac{x_0-0.1a}{a})comb(\frac{y_0}{a})$

这里可以傅里叶变换得到其频谱为：

$\begin{aligned} T(f_x,f_y) &=a^2 [comb(af_x) comb(af_y)]+a^2 e^{-j0.2 \pi af_x}[comb(af_x) comb(af_y)] \\ &= a^2[1+e^{-j0.2 \pi af_x}][comb(af_x)comb(af_y)] \end{aligned}$

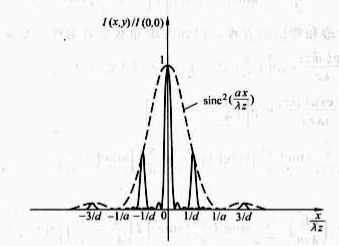
代入夫琅禾费公式：

$\begin{aligned} U(x,y)&=\frac{1}{j \lambda z}e^{jkz}e^{j\frac{k}{2z}(x^2+y^2)}\mathscr{F}\{U_o(f_x,f_y)\}|_{f_x=\frac{x}{\lambda z},f_y=\frac{y}{\lambda z}} \\ &= \frac{1}{j \lambda z}e^{jkz}e^{j\frac{k}{2z}(x^2+y^2)}T(\frac{x}{\lambda z},\frac{y}{\lambda z}) \\ &= \frac{1}{j \lambda z}e^{jkz}e^{j\frac{k}{2z}(x^2+y^2)} \cdot a^2[1+e^{-j0.2 \pi af_x}][comb(af_x)comb(af_y)] \end{aligned}$

注：这里得到的已经是复振幅强度对坐标(x,y)的分布了，而不是对频率对$(f_x,f_y)$的分布。

这就是z处的夫琅禾费衍射复振幅分布函数了，但通常人眼和探测器都仅仅对衍射强度敏感，所以我们求得其功率谱分布：

$\begin{aligned} I(f_x,f_y) &= \mid U(f_x,f_y) \mid^2 \end{aligned}$

附录

本例中用到的常用 Katex 表达式

$a \cdot b$ --> $a \cdot b$

$$\mathscr{F} = $$ --> $\mathscr{F}$

$$\boxed{...}$$ --> \boxed{ABC}