Matlab中的lambda表达式 f=@(x) x^2-2*x+1;
Matlab中的lambda表达式
f=@(x) x^2-2*x+1;
基于MATLAB的矩阵及元素赋值
基于MATLAB的矩阵及元素赋值_人工智能_huyaping2014的专栏-CSDN博客
艾特小蘑菇 2019-03-10 10:13:11  4562
4562 
 收藏 4
收藏 4
最后发布:2019-03-10 10:13:11首发:2019-03-10 10:13:11
*内容摘要 :该代码用于实现在MATLAB中矩阵及元素的赋值
*文件标识:无
*作 者: *完成日期:2019-3-10
*问题描述:给矩阵a赋值
>> a=[1 4 7;2 5 8; 3 6 9]
a =
1 4 7
2 5 8
3 6 9
*问题描述:给矩阵全行赋予值
*例如给矩阵的第5行赋值为【2 4 6 】
>> a(6,:)=[2 4 6]
a =
1 4 7
2 5 8
3 6 9
0 0 0
0 0 0
2 4 6
*问题描述:要把矩阵的第3,4行及1,3列交点上的元素取出,构成一个新的矩阵
>> b=a([3 4],[1 3])
b=
3 9
0 0
>> f1=ones(3,4)
*问题描述:实现全1矩阵f1;实现全0矩阵f2;实现魔方矩阵f3;实现单位矩阵f4.
f1 =
1 1 1 1
1 1 1 1
1 1 1 1
>> f2=zeros(3,4)
f2 =
0 0 0 0
0 0 0 0
0 0 0 0
>> f3=magic(3)
f3 =
8 1 6
3 5 7
4 9 2
>> f4=eye(3)
f4 =
1 0 0
0 1 0
0 0 1
>>
MATLAB基础学习(二)-变量类型与赋值

杨广帅 2018-09-11 10:06:36  19475
19475 
 收藏 18
收藏 18
最后发布:2018-09-11 10:06:36首发:2018-09-11 10:06:36
分类专栏: MATLAB
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
本文链接:https://blog.csdn.net/weixin_42717711/article/details/82620634
展开
matlab解决问题的最基本思路是建立脚本文件,那么脚本文件的第一段就是定义一些变量,这和C语言等编程思想是一样的。matlab提供的变量类型很多,最基础的是三种:数值变量、符号变量、字符串,其他的类型还有cell、table等。这里仅说明最基础的变量类型。
1.数值变量
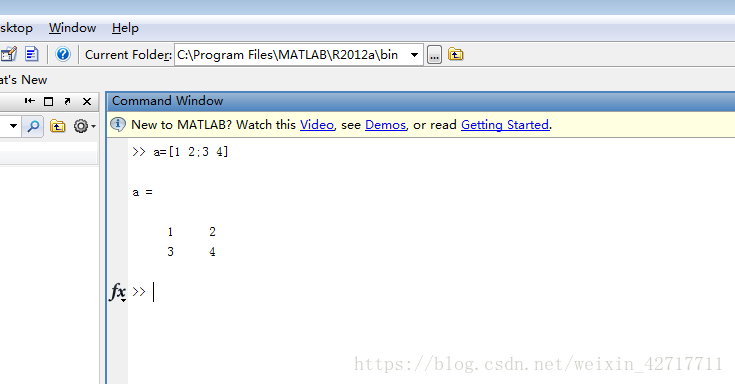
matlab中所有的数值变量都是矩阵,赋值时,以方括号作为开头和结尾,以英文逗号或空格分割同行元素,以英文分号分割各列。例如在Command Window里输入
a=[1 2;3 4]
可以看到运算结果,a是一个数值变量。同时workspace里出现一个田字形的变量a,说明变量a的类型是数值型。
向量和数字可以视为特殊的矩阵,例如
a=[1 2]
a=[1;2]
分别是行向量和列向量。
a=[1] 可以简写为a=1 是数字。
数值变量的命名要求是英文字母开头,不能包含特殊符号,大小写敏感。这里推荐采用下划线来进行分割,例如value_of_A,这和其他编程语言的命名规则大体相当。
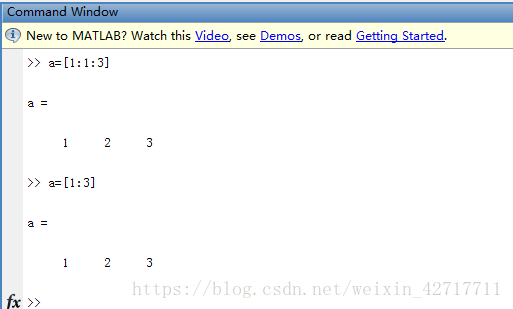
赋值中,有时需要用到等差数列,例如定义一个向量a=[1 2 3],如果比较长,赋值很麻烦,所以matlab提供了一个简单的方法
a=[1:1:3]
这里两个冒号的意思是起始值:步长:终值。采用这种赋值方式时可以获得一个等差数列行向量,并可以省略两侧的方括号。当步长为1时,可以省略步长和一个冒号,于是可以简写为
- a=1:3
另一种灵活的赋值方法是分块矩阵,其方法是变量名后面加圆括号,圆括号中加序号。例如
a=[1 2;3 4]
定义变量a之后,
b=a(1,2)
就可以把a的第一行第二列元素赋值给b,当然也可以用
a(1,2)=1
来修改矩阵中部分元素的值。这里需要注意,序号必须是自然数,且不能是零。当矩阵中有多个元素需要赋值时,可以将序号部分改成向量,例如
a([1 2],[1 2])=[1 2;3 4]
中把行数和列数都用向量表示,就是说对矩阵a的第1和2行,第1和2列,总共4个元素赋值。更进一步,也可以有a([1 2],1)表示a的第一列,也可以写成
a(1:end,1)
这里的end表示终点,即a的行数2,也可以更进一步简写成
a(:,1)
这里的冒号表示从头至尾。这类赋值方法最为常用,但基本的语法非常简单,方括号表示矩阵开头和结尾,圆括号表示从矩阵中选取部分,把握这个原则,有利于读懂程序。
当然分块矩阵也可以
b=[a a]
这样的赋值方法,但需要注意的是,方括号中的元素必须满足矩阵的行列数要求,例如
a=[1 1]
b=[1;1]
c=[a b]
就会引起错误,因为此时matlab无法确定c的行列数。
2.符号变量
总体而言,符号变量比数值变量简单得多,因为变化非常少,常用的赋值命令是
syms a b
syms表示这里要定义一些符号变量,a和b是变量名,符号变量的命名规则和数值变量一样。有时候也采用
syms a real
来强调a是实数变量,具体可以doc syms来获得帮助。
有些变量之间存在依赖关系,此时可以定义
syms x y(x)
这里声明x是一个符号变量,又声明y是一个符号变量,且y的值由x决定,这相当于数学中函数的概念。当然具体的函数关系并没有明确规定。也可以
syms x y z(x,y)
来定义符号变量z,z依赖x和y。这相当于二元函数的概念。这里的圆括号显然和数值变量中的圆括号含义完全不同,这也是学习matlab最不习惯的地方,同一个符号,由于变量类型不同会有完全不同的含义。所以在学习matlab的过程中,一定要区分数值变量和符号变量。
上述方法定义的符号变量是一个数,或者1*1矩阵,matlab中也可以定义符号矩阵,例如
syms a11 a12 a21 a22
A=[a11 a12;a21 a22]
就可以获得一个矩阵符号变量A。
定义符号变量后,workspace中出现相应的变量名,图形不是数值变量的田字形,而是方框里有个立方体,双击后可以看到行列数。
3.字符串
比数值、符号更为简单的就是字符串了,其定义方法是以单引号开头和结尾,例如
a=‘hello world’
就定义了一个字符串a,其值为你好世界。matlab中较为特殊的是,字符串可视为行向量,例如
- b='hello ’
- c=‘world’
- a=[b c]
也可以获得字符串a,其值为你好世界。另外,有时也可以将字符串视为矩阵,例如
a=[‘ab’;‘cd’]
但这种用法很罕见,同时要求各行字符串长度一样,否则将违反矩阵行列数规定。
当然字符串的值也可以是特殊符号,比如
- ',
就定义了逗号,而最特殊的就是定义单引号,因为单引号会和字符串定义中的单引号混淆,因此matlab中用两个单引号表示一个单引号,也就是
- a=’’’’
表示a是一个字符变量,值是一个单引号。语句中第一和第四个单引号是字符串类型的开头和结尾,中间两个单引号用来表示一个单引号。
定义字符串变量后,workspace中出现相应的变量名,图像是方框里写了ch,双击后可以看到行列数。
matlab 判断对象的数据类型isa()_人工智能_CSDN1HAO的博客-CSDN博客blog.csdn.net
“参量obj是一个MATLAB对象或者Java对象。参量class_name是MATLAB(预定义的或用户定义的)对象或Java对象。预定义的MATLAB对象包括如下类型:logical 逻辑数组char 字符串数组numeric 整型或浮点型数组integer 有符号或无符号整型数组… ”
7Matlab 如何将矩阵中的数分别赋值给多个变量_人工智能…_CSDN博客
2018年8月13日 - matlab同时给多个变量赋值例子1:对x,y,z同时初始化为100例子2:对a,b,c分别初始化为mat,lab,sky例子3:将Cell数组x={123}中的1,2,3分别赋值给a,b,c例子…
[转载]MATLAB中一条语句给多个变量赋值(转载)
(2017-10-08 17:51:31)
对a,b和c分别赋值1,2和3
a,b,c=1,2,3
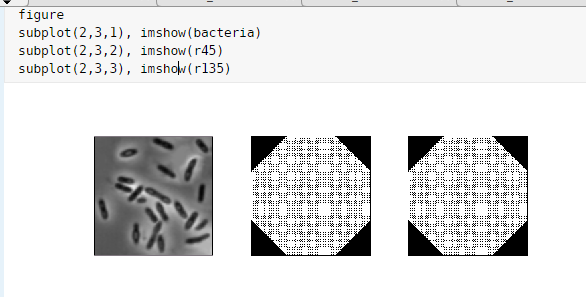
一些图像变换矩阵
图像几何变换

DL_fan 2018-10-09 14:18:52  5887
5887 
 收藏 6
收藏 6
最后发布:2018-10-09 14:18:52首发:2018-10-09 14:18:52
分类专栏: opencv
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
本文链接:https://blog.csdn.net/fanzonghao/article/details/82981560
展开
一.仿射变换概念
1.下图是一般形式,其中x,y代表原坐标,v,w代表变换后的坐标,T是变换矩阵
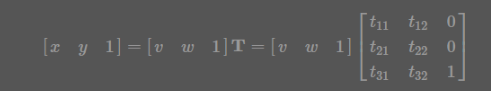
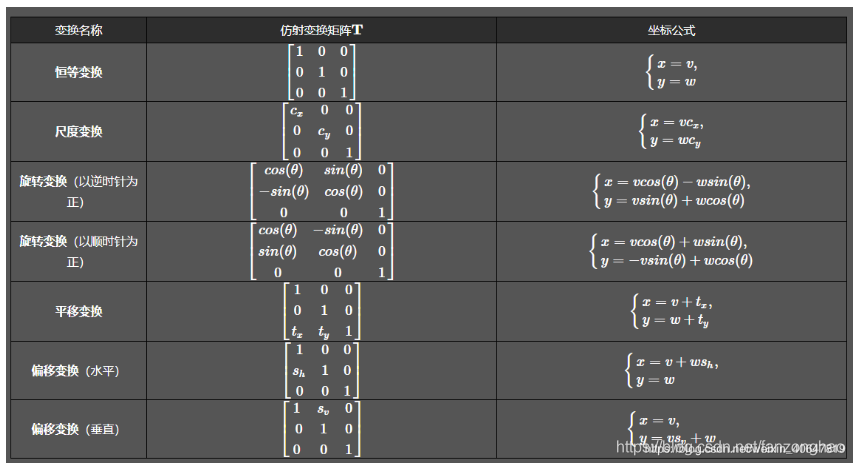
其中几种常见的变换形式矩阵为:
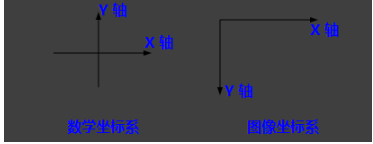
2.坐标系变换
再看第二个问题,变换中心,对于缩放、平移可以以图像坐标原点(图像左上角为原点)为中心变换,这不用坐标系变换,直接按照一般形式计算即可。而对于旋转和偏移,一般是以图像中心为原点,那么这就涉及坐标系转换了。
我们都知道,opencv的原点在图像左上角,水平向右为 X 轴,垂直向下为 Y 轴。课本中常见的坐标系是以图像中心为原点,水平向右为 X 轴,垂直向上为 Y 轴,称为笛卡尔坐标系。看下图:
因此,对于旋转和偏移,就需要3步(3次变换):
- 将输入原图图像坐标转换为笛卡尔坐标系;
- 进行顺时针旋转计算。旋转矩阵前面已经给出了;
- 将旋转后的图像的笛卡尔坐标转回图像坐标。
3.示例:(250,0)绕(250,250)旋转120度
import cv2
import numpy as np
from math import cos,sin,pi
def rotate_one(x,y,angle,cx,cy):
"""
点(x,y) 绕(cx,cy)点顺时针旋转
"""
angle = angle*pi/180
x_new = (x-cx)*cos(angle) + (cy-y)*sin(angle)+cx
y_new = (x-cx)*sin(angle) + (y-cy)*cos(angle)+cy
return x_new, y_new
def rotate_two(x,y,angle,cx,cy):
"""
点(x,y) 绕(cx,cy)点顺时针旋转
"""
angle = angle * pi / 180
input_matrix = np.array([x, y, 1])
transform_matrix = np.array([[1, 0, 0],
[0, -1, 0],
[-cx, cy, 1]])
inv_transform_matrix = np.array([[1, 0, 0],
[0, -1, 0],
[cx, cy, 1]])
rotate_matrix = np.array([[cos(angle), -sin(angle), 0],
[sin(angle), cos(angle), 0],
[0, 0, 1]])
output_matrix = ((input_matrix.dot(transform_matrix)).dot(rotate_matrix)).dot(inv_transform_matrix)
x_new, y_new, _ = output_matrix
return x_new, y_new
def test_cv2():
img=np.zeros((501,501))
x, y= 250, 0
cx,cy=250,250
angle=120
# x_new, y_new = rotate_one(x,y,angle,cx,cy)
# cv2.circle(img,(x,y),radius=2,color=(255,255,255),thickness=2)
# cv2.circle(img, (cx, cy), radius=2, color=(255, 255, 255), thickness=2)
# cv2.circle(img, (int(x_new), int(y_new)), radius=2, color=(255, 255, 255), thickness=2)
# cv2.imshow('img', img)
# cv2.waitKey(0)
x_new, y_new = rotate_two(x,y,angle,cx,cy)
cv2.circle(img,(x,y),radius=2,color=(255,255,255),thickness=2)
cv2.circle(img, (cx, cy), radius=2, color=(255, 255, 255), thickness=2)
cv2.circle(img, (int(x_new), int(y_new)), radius=2, color=(255, 255, 255), thickness=2)
cv2.imshow('img', img)
cv2.waitKey(0)
if __name__ == '__main__':
test_cv2()

4.代码示例:对图中的最大轮廓猪猪旋转180度
import cv2
import numpy as np
from math import cos,sin,pi
import imutils
from matplotlib import pyplot as plt
def rotate(points, angle, cx, cy):
"""
点(x,y) 绕(cx,cy)点顺时针旋转
"""
h, w = points.shape
one = np.ones((h, 1))
input_matrix = np.hstack((points,one))
print(input_matrix.shape)
print(input_matrix[:2])
angle = angle * pi / 180
# input_matrix = np.array([x, y, 1])
transform_matrix = np.array([[1, 0, 0],
[0, -1, 0],
[-cx, cy, 1]])
inv_transform_matrix = np.array([[1, 0, 0],
[0, -1, 0],
[cx, cy, 1]])
rotate_matrix = np.array([[cos(angle), -sin(angle), 0],
[sin(angle), cos(angle), 0],
[0, 0, 1]])
output_matrix = ((input_matrix.dot(transform_matrix)).dot(rotate_matrix)).dot(inv_transform_matrix).astype(np.int)
# print(output_matrix.shape)
# print(output_matrix[:2])
# x_new, y_new, _ = output_matrix
return output_matrix[:, :-1]
def test_pig_rotate():
path = './20181011234118419.jpeg'
img = cv2.imread(path)
gary = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
black=np.zeros([img.shape[0], img.shape[1]])
#二值化找轮廓
image_thre = cv2.threshold(gary, 127, 255, cv2.THRESH_BINARY)[1]
cnts = cv2.findContours(image_thre, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
contours = cnts[0] if imutils.is_cv2() else cnts[1]
c_ = sorted(contours, key=cv2.contourArea, reverse=True)
points = np.squeeze(c_[0])
# #debug show
plt.figure(figsize=(15,15))
# plt.plot(points[:, 0], points[:, 1])
# plt.show()
contour_list = []
new_points = rotate(points, angle=120, cx=img.shape[1]//2, cy=img.shape[0]//2)
contour_list.append(new_points[:, np.newaxis, :])
black = cv2.drawContours(black, contour_list, -1, (255, 255, 255), thickness=-1)
cv2.imwrite('./3.jpg', black)
if __name__ == '__main__':
# test_cv2()
test_pig_rotate()
原图:

顺时针旋转180度:

5.代码示例:对整张图进行旋转
# 旋转图片无黑边
def rotate_image():
from math import fabs
from math import sin, cos, radians
path = './20181011234118419.jpeg'
img = cv2.imread(path)
# img=cv2.imread('2018-09-10IMG_8003.jpg')
height, width = img.shape[:2]
degree = 90
# 旋转后的尺寸
heightNew = int(width * fabs(sin(radians(degree))) + height * fabs(cos(radians(degree))))
widthNew = int(height * fabs(sin(radians(degree))) + width * fabs(cos(radians(degree))))
matRotation = cv2.getRotationMatrix2D((width / 2, height / 2), degree, 1)
# print(matRotation[0, 2])
# print(matRotation)
matRotation[0, 2] += (widthNew - width) / 2
matRotation[1, 2] += (heightNew - height) / 2
imgRotation = cv2.warpAffine(img, matRotation, (widthNew, heightNew), borderValue=(255, 255, 255))
#
# cv2.imshow('img', imgRotation)
# cv2.waitKey(0)
cv2.imwrite('img_size_1_ok.jpg', imgRotation)
if __name__ == '__main__':
rotate_image()


旋转矩阵:
\left[ \begin{array}{cc} s_x & 0&0\ 0 & x_Y & 0 \ 0 & 0 & 1 \end{array}\right]
matlab 从已有矩阵构造新矩阵
matlab 显示变量信息
whos A
returns
Name Size Bytes Class Attributes
A 1x1 8 double
matlab 扩充矩阵维度
matlab多维数组操作
1.一个三维数组由行、列和页三维组成,其中每一页包含一个由行和列构成的二维数组。
2.利用标准数组函数创建多维数组
A=zeros(4,3,2) 生成一个4行3列2页的三维全0数组,ones,rand和randn等函数有相似的用法。
3.利用直接索引方式生成多维数组
A=zeros(2,3)
A(:,:,2)=ones(2,3)
A(:,:,3)=4
上面的代码先生成一个二维数组作为三维数组的第一页,然后通过数组直接索引,添加第二页、第三页。
4.利用函数reshape和repmat生成多维数组
B=reshape(A,2,9)
B=[A(:,:,1) A(:,:,2) A(:,:,3)] %结果与上面一样。
reshape(B,2,3,3)
reshape(B,[2 3 3]) %结果与上面一样。
提示:reshape函数可以将任何维数的数组转变成其他维数的数组。
5.利用repmat函数生成多维数组
C=ones(2,3)
repmat(C,[1 1 3]) % repmat写出类似reshape的repmat(C,1,1,3)将显示出错
提示:repmat是通过数组复制创建多维数组的,上面的代码即是将数组C在行维和列维分别复制一次,然后再页维复制三次得到2×3×3的三维数组。
6.利用cat函数创建多维数组
a=zeros(2);
b=ones(2);
c=repmat(2,2,2);
D=cat(3,a,b,c)%创建三维数组
D=cat(4,a,b,c) %创建4维数组。
D(:,1,:😅 %查看第一列的数据。
size(D) %可以知道数组D的具体维数。
6.数组运算与处理
数组之间的运算要求两个数组在任何一维都必须具有相同的大小。
(1)squeeze函数用于删除多维数组中的单一维(即大小为1的那些维)
E=squeeze(D)
size(D) E的数据和D一样,但比D少了一维,只有2行、2列和3页。
(2)reshape函数可以将一个三维向量变成一维向量。
v(1,1,:)=1:6
squeeze(v)
v(😃
(3)reshape函数用于改变多维数组的行、列、页以及更高阶的维数,但不改变数组元素的总个数。
F=cat(3,2+zeros(2,4),ones(2,4),zeros(2,4))
G=reshape(F,[3,2,4])
H=reshape(F,[4 3 2]) 或K=reshape(F,2,12)
多维数组的重组按这样的顺序:第一页的第一列、第二列……,第二页的第一列、第二列……。
7.sub2ind函数和ind2sub函数用于多维数组的直接引用,索引顺序与重组顺序一致。
sub2ind(size(F),1,1,1) %求第1行、第1列、第1页的数值的单一索引
sub2ind(size(F),1,2,1) %求第1行、第2列、第1页的数值的单一索引
sub2ind(size(F),1,2,3) %求第1行、第2列、第3页的数值的单一索引
[r c p]=ind2sub(size(F),19) %由单一索引求其对应的行列页数值。
8.函数flipdim用于多维数组的翻转,相当于二维数组中的flipud和fliplr函数。例如下面的代码进行按行、列和按页翻转。
M=reshape(1:18,2,3,3)
flipdim(M,1) %每一页中的行翻转
flipdim(M,2) %每一页中的列翻转
flipdim(M,3) %将第一和第三页翻转调换
9.函数shiftdim用于循环轮换一个数组的维数。如果一个数组r行、c列和p页,则循环轮换一次,就生成一个c行、p列和r页的数组。
M %重新调用
shiftdim(M,1) %轮换一次
shiftdim(M,2) %轮换两次
数组轮换后规律很难直观理解,我们可以将三维数组看成一个类似魔方的方形盒子
函数shiftdim也支持负的循环轮换次数。执行该轮换时,数组的维数增加,并且多出的维数均为单一维。
M %重新调用
size(M)
shiftdim(M,-1)
size(ans).
10.函数permute和ipermute用于实现多维条件下的转置操作。从本质上讲permute函数是shiftdimhas函数的扩展。
M %重新调用
permute(M,[2 3 1])
shiftdim(M,1) %两者结果一样
permute函数中的参数[2 3 1]表示使函数第二维成为第一维,第三维成为第二维,第一维成为第三维。
11. permute(M,[2 1 3])
[2 1 3]表示将数组的行列相互转置,页保持不变(只在第一和第二维转置)。
permute函数的第一个参数为待转置的数组,第二个参数为转置顺序,它必须是待转置的多维数组的维数的某种排列,否则所进行的转置无法进行。
permute函数也可以用来将一个数组变成更高维的数组,例如shiftdim(M,-1)也可以用permute函数来实现。
permute(M,[4 1 2 3])
这是 因为任何一个数组都具有大于其本身尺寸的更高维数,并且这些维数均为单一维数。例如二维数组具有页这一维,只是只有一页。总之超过数组本身大小的维数都是单一维。M是一个三维数组,其第四维必为单一维,因此将M的第四维与第一维转置,第一维变成了单一维。
12.二维数组两次转置变换回原来的形式,对于多维数组,用函数ipermute来取消permute所执行的转置操作。
M %重新调用
permute(M,[3 2 1])
ipermute(M,[3 2 1]) %在我的Matlab上运行没有达到预期效果
13.size函数返回数组每一维的大小
numel函数返回数组的总元素个数
当不指定size的返回值时,将返回一个由数组的各维数组成的向量。当我们知道数组的维数时,可以将维数返回到指定变量中。
[r c p]=size(M)
r=size(M,1)
c=size(M,2)
p=size(M,3)
v=size(M,4)
当一个数组的维数或者某数组维数不确定时,可以利用函数ndims获得数组的维数值。例如:ndims(M),与length(size(M))等效。
matlab 求逆矩阵 inv(A)
缩放矩阵:
scale = @(sx, sy) [sx,0,0;0,sy,0;0,0,1];
M1 = scale(0.5, 1.2);
M1 =
0.5000 0 0
0 1.2000 0
0 0 1.0000
进行坐标变换:
p = [1,2,3];
p1 = M1 * p';
输出的坐标为:
p1 =
0.5000
2.4000
3.0000
使用inv,求逆矩阵,对坐标进行逆变换:
p2 = inv(M1)*p1;
输出:
p2 =
1
2
3








 CSDN技术社区
CSDN技术社区


