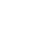【CS】有限状态机（FSM）模型

什么是有限状态机？

什么是状态机（State Mechine）？顾名思义，即一种可以在一些状态中进行转换的机器，显然这仅仅是一种理想模型，并没有考虑具体的实现方式。

定义

有限状态机，（英语：Finite-state machine, FSM），又称有限状态自动机，简称状态机，是表示有限个状态以及在这些状态之间的转移和动作等行为的数学模型。

有什么用？

虽然听起来仅仅是一个不沾边、不实用、不靠谱的理论模型，但在生活中的例子实在太多了，状态机模型广泛可见于机械结构、电子元件、计算机编程算法当中，只要是在确定的状态间切换的逻辑，都可以归纳为状态机模型。

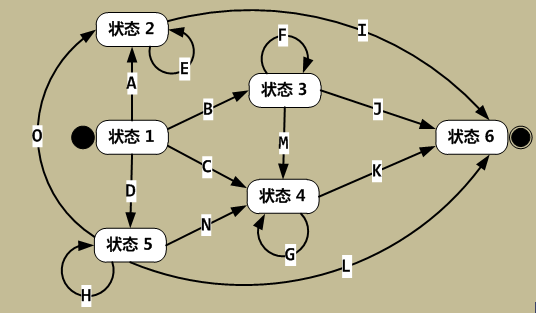
有限状态机是一种用来进行对象行为建模的工具，其作用主要是描述对象在它的生命周期内所经历的状态序列，以及如何响应来自外界的各种事件。在计算机科学中，有限状态机被广泛用于建模应用行为、硬件电路系统设计、软件工程，编译器、网络协议、和计算与语言的研究。比如下图非常有名的TCP协议状态机。

状态机模型

有限状态机一般都有以下特点：

1. 可以用状态来描述事物，并且任一时刻，事物总是处于一种状态；
2. 事物拥有的状态总数是有限的；
3. 通过触发事物的某些行为，可以导致事物从一种状态过渡到另一种状态；
4. 事物状态变化是有规则的，A状态可以变换到B，B可以变换到C，A却不一定能变换到C；
5. 同一种行为，可以将事物从多种状态变成同种状态，但是不能从同种状态变成多种状态。

状态

状态机可归纳为4个要素，即现态、条件、动作、次态。“现态”和“条件”是因，“动作”和“次态”是果。详解如下：

现态：

指当前所处的状态。

次态：

条件满足后要迁往的新状态。“次态”是相对于“现态”而言的，“次态”一旦被激活，就转变成新的“现态”了。

状态转换动作条件

状态机在满足触发条件时进行状态切换，如当计数达到指定大小进行下一个阶段操作。

条件：

又称为“事件”。当一个条件被满足，将会触发一个动作，或者执行一次状态的迁移。

动作：

条件满足后执行的动作。动作执行完毕后，可以迁移到新的状态，也可以仍旧保持原状态。动作不是必需的，当条件满足后，也可以不执行任何动作，直接迁移到新状态。

状态机的描述

状态机模型可以使用关系表达式（状态方程）、状态转换图、状态转换表等多种方式进行描述。

状态转换图

STD图(State Transform Diagram)状态转换图,表示行为模型。STD通过描述系统的状态和引起系统状态转换的事件，来表示系统的行为，指出作为特定事件的结果将执行哪些动作（例如，处理数据等）。STD描述系统对外部事件如何响应，如何动作。

通过描绘系统的状态及引起系统状态转换的事件，来表示系统的行为。此外状态转换图还指明了作为特定事件的结果系统将做哪些动作（例如，处理数据）。因此状态转换图提供了行为建模机制。

在状态转换图中，每一个节点代表一个状态，其中双圈是终结状态。许多单片机教材上对工作模式的表达通常采用状态图的形式。

状态转换表

状态机模型可以用状态转换表来简化状态切换逻辑，因为只要输入变量处于确定状态，其输出也应当是一个确定态，也即状态互转可以使用输入/输出一一对应关系表来描述。

应用举例

例1. TCP状态转换图

例2. JavaScript中对用户鼠标状态的交互动作

在js中，新建一个对象，用这个对象的属性来模拟元素的状态,用这个对象的方法模拟元素在不同状态的转变,那么这个对象就是一个有限状态机。是否可用有限状态机来描述，却决于：当前状态确定，有限个状态，响应事件，在不同状态间有规律的转变。它对JavaScript的意义在于，很多对象可以写成有限状态机。举例来说，网页上有一个菜单元素。鼠标悬停的时候，菜单显示；鼠标移开的时候，菜单隐藏。如果使用有限状态机描述，就是这个菜单只有两种状态（显示和隐藏），鼠标会引发状态转变。

var menu = {
    // 当前状态
    currentState: 'hide',
    // 绑定事件
    initialize: function() {
        var self = this;self.on("hover", self.transition);
    },
    // 状态转换
    transition: function(event){
        switch(this.currentState) {
            case "hide":
                this.currentState = 'show';
                doSomething();
                break;
            case "show":
                this.currentState = 'hide';
                doSomething();
                break;
            default:
                console.log('Invalid State!');
                break;
        }
    }
};

可以看到，有限状态机的写法，逻辑清晰，表达力强，有利于封装事件。一个对象的状态越多、发生的事件越多，就越适合采用有限状态机的写法。另外，JavaScript语言是一种异步操作特别多的语言，常用的解决方法是指定回调函数，但这样会造成代码结构混乱、难以测试和除错等问题。有限状态机提供了更好的办法：把异步操作与对象的状态改变挂钩，当异步操作结束的时候，发生相应的状态改变，由此再触发其他操作。这要比回调函数、事件监听、发布/订阅等解决方案，在逻辑上更合理，更易于降低代码的复杂度。

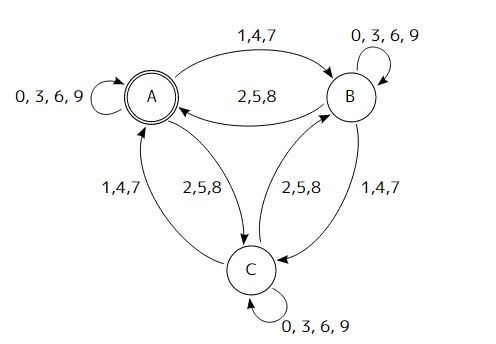
例3. 正则表达式: 匹配所有3的倍数

使用如下pattern可以匹配文本中的独行文本中的3的整数倍数字。

^[0369]*(([147][0369]*|[258][0369]*[258][0369]*)([147][0369]*[258][0369]*)*([258][0369]*|[147][0369]*[147][0369]*)|[258][0369]*[147][0369]*)*$

这个正则是真正正确的，适用于任意十进制数，而不是下面那样作弊的手段。
从下面这个有限自动机逆变得到：

^[0369]* (
  (
    [147][0369]*
  | [258][0369]*[258][0369]*
  ) ([147][0369]*[258][0369]*)* (
    [258][0369]*
 
  | [147][0369]*[147][0369]*
  )
| [258][0369]*[147][0369]* )* $

其实，写一个正则匹配 10 进制下 n 的倍数的思路是这样：构造一个有 n 个状态的 DFA，状态为$q_0,q_1, ..., q_{n-1}$，其中起始和接受状态都是$q_0$。DFA 中$q_k$的含义是「当前读入的数可以被 n 除余 k」。
对每个$q_k$和$m\in\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}$，计算$r=(10k+m)\ \mathrm{mod}\ n$，构造一条q_k\xrightarrow{m} q_r的转移边这张 DFA 就可以匹配能被 n 整除的十进制数。下面是被 7 整除的十进制数的正则，长达 12000 余字：

0|(7|[18]5*4|(2|9|[18]5*6)(3|[29]5*6)*(1|8|[29]5*4)|(3|[18]5*[07]|(2|9|[18]5*6)(3|[29]5*6)*(4|[29]5*[07]))(1|8|65*[07]|(0|7|65*6)(3|[29]5*6)*(4|[29]5*[07]))*(5|65*4|(0|7|65*6)(3|[29]5*6)*(1|8|[29]5*4))|(4|[18]5*[18]|(2|9|[18]5*6)(3|[29]5*6)*(5|[29]5*[18])|(3|[18]5*[07]|(2|9|[18]5*6)(3|[29]5*6)*(4|[29]5*[07]))(1|8|65*[07]|(0|7|65*6)(3|[29]5*6)*(4|[29]5*[07]))*(2|9|65*[18]|(0|7|65*6)(3|[29]5*6)*(5|[29]5*[18])))(6|35*[18]|(4|35*6)(3|[29]5*6)*(5|[29]5*[18])|(5|35*[07]|(4|35*6)(3|[29]5*6)*(4|[29]5*[07]))(1|8|65*[07]|(0|7|65*6)(3|[29]5*6)*(4|[29]5*[07]))*(2|9|65*[18]|(0|7|65*6)(3|[29]5*6)*(5|[29]5*[18])))*(2|9|35*4|(4|35*6)(3|[29]5*6)*(1|8|[29]5*4)|(5|35*[07]|(4|35*6)(3|[29]5*6)*(4|[29]5*[07]))(1|8|65*[07]|(0|7|65*6)(3|[29]5*6)*(4|[29]5*[07]))...

下面教你怎么把 DFA 转正则：

还是从它开始

我们记 A 为终止到状态 A 的字符串集合，BC 类似，那么可以列出三个方程：

A = A[0369] | B[258] | C[147] |
B = A[147] | B[0369] | C[258]
C = A[258] | B[147] | C[0369]

根据正则语言的特性，可以推导出如下形式的方程L = LU|V有解L = VU*因此上面方程可以修改为

B = (A[147] | C[258])[0369]* (2)
C = (A[258] | B[147])[0369]* (3)

将 (3) 代入 (1) (2) 得A = (| B[258] | (A[258] | B[147])[0369][147])[0369] (4)
B = (A[147] | (A[258] | B[147])[0369][258])[0369] (5)用分配律展开 (5) 中的竖线得到

B = A[147][0369]* | A[258][0369]*[258][0369]* | B[147][0369]*[258][0369]*

故

B = A[147][0369]*([147][0369]*[258][0369]*)* 
  | A[258][0369]*[258][0369]*([147][0369]*[258][0369]*)*

把它代入 (4) 得

  =   [0369]* 
    | B[258][0369]*
    | A[258][0369]*[147][0369]*
    | B[147][0369]*[147][0369]* 
  =   [0369]* 
    | A[147][0369]*([147][0369]*[258][0369]*)*[258][0369]*
    | A[258][0369]*[258][0369]*([147][0369]*[258][0369]*)*[258][0369]*
    | A[258][0369]*[147][0369]*
    | A[147][0369]*([147][0369]*[258][0369]*)*[147][0369]*[147][0369]* 
    | A[258][0369]*[258][0369]*([147][0369]*[258][0369]*)*[147][0369]*[147][0369]* 
  = [0369]* (
                  [147][0369]*([147][0369]*[258][0369]*)*[258][0369]*
    | [258][0369]*[258][0369]*([147][0369]*[258][0369]*)*[258][0369]*
    |             [147][0369]*([147][0369]*[258][0369]*)*[147][0369]*[147][0369]* 
    | [258][0369]*[258][0369]*([147][0369]*[258][0369]*)*[147][0369]*[147][0369]*
    | [258][0369]*[147][0369]* )*
  = [0369]* (
      (
        [147][0369]*
      | [258][0369]*[258][0369]*
      ) ([147][0369]*[258][0369]*)* (
        [258][0369]*
 
      | [147][0369]*[147][0369]*
      )
    | [258][0369]*[147][0369]* )*

加上 ^ 和 $ 就行了，放去测试，全部正确。