【信息光学】第五章 光学成像系统的频率特性

dexfire · 2020-3-20 · 次阅读

【信息光学】第五章 光学成像系统的频率特性

5.0 物理光学

光学信息：

  • 物理层面：频率、振幅、相位
  • 感官层面：颜色 -> 色调、亮度
  • 宏观感受：对比度、亮度、饱和度、锐度

光波

光波的表达式

平面波：

E=E0e−j(wt−kr)E = E_0e^{-j(wt-kr)}

光学参数

振幅

时间频率

空间频率，波长

偏振

  • 只有横波才有偏振方向之分，而纵波的震动方向始终与传播方向相同，不存在偏振。
  • 对于平面波，其振动方向

成像光学基础

常见光波形式

球面波

复振幅表达式( 距原点 z处的 xOy平面 ):

E(x,y)=E0ze−j(w⋅t−k⋅r)E(x,y) = \frac{E_0}{z}e^{-j(w \cdot t-k \cdot r)}

5.1 透镜的成像性质

透镜是用透明物质制成的表面为球面一部分的光学元件，镜头是由几片透镜组成的，有塑胶透镜（plastic）和玻璃透镜（glass）两种，玻璃透镜比塑胶贵。

成像

U_

  • 成像是指照明一个放置于透镜之前的物体，使其经由透镜在另一位置，出现与物体非常相似的光场强度分布。
  • 这个强度分布称之为该物体的像。
  • 可以用光屏接收的实际强度分布，称为实像。
  • 如果透镜后方的光可等效与透镜前另一个位置发出的，称之为虚像。

理想成像

理想的透镜成像系统，对入射光波在像面上进行还原：
假设输入光波为：

U(x,y)=A0∑n=1Nejk(xcosαn+ycosβn)=A0∑n=1Nejk()\begin{aligned} U(x,y) &= A_0\sum_{n=1}^{N} e^{jk(x \cos \alpha_n + y \cos \beta_n)} \\ &= A_0 \sum_{n=1}^{N} e^{jk\left( \right)} \end{aligned}

U(x,y)=A0∑n=1Nδ(xλz−an,yλz−bn)U(x,y) = A_0\sum_{n=1}^{N} \delta \left( \frac{x}{\lambda z}-an,\frac{y}{\lambda z}-bn \right)

则

受限衍射系统：

  • 例题1：

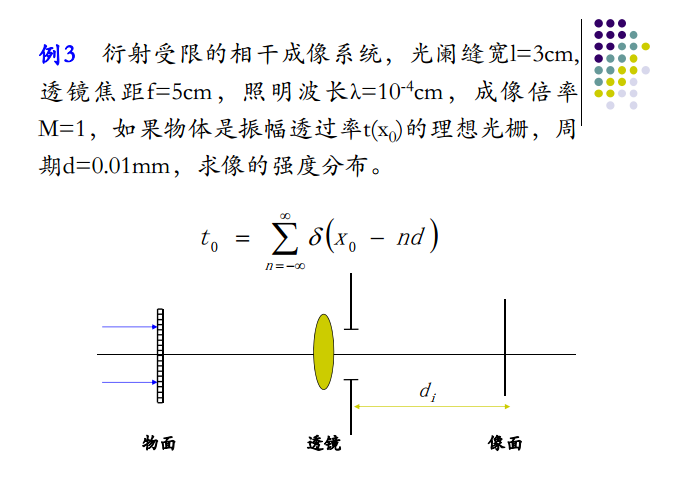
解题思路：

  1. 先求透镜理想像的幅度表达式：Ug(x,y)\displaystyle U_g(x,y)
  2. 再求得孔径的傅里叶变换。
  3. 输出频谱：Ui(fx,fy)=G(fx,fy)⋅H(fx,fy)\displaystyle U_i(f_x,f_y) = G(f_x,f_y) \cdot H(f_x,f_y)


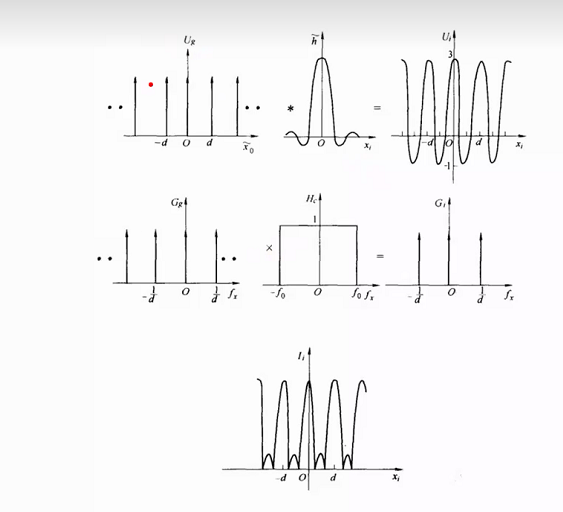
  • 例题2：


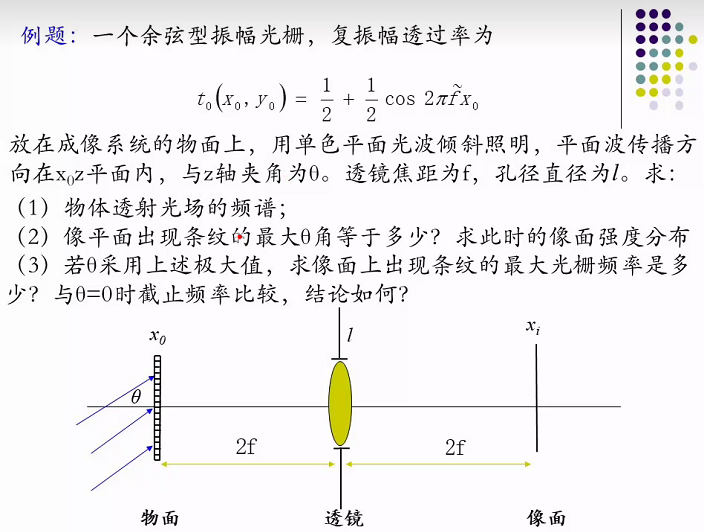
注：这里由于是与z轴夹角，所以代入sinθ\sin \theta。
光波斜入射引入的位相因子，ejkx0e^{jkx_0} -> ejksinθx0e^{jk\sin \theta x_0}


像频谱：是经过出瞳函数进行带通滤波后的物像，必须要有物体的频率成分通过。

注：常考题型，物面、像变、输入光波变化后，分析截止频率的变化。

相干照明系统的传递函数（CTF）

HC(fx,fy)H_C(f_x,f_y)

非相干照明系统的传递函数（OTF）

H(fx,fy)H(f_x,f_y)

由自相干定理。

H(fx,fy)=P(λdifx,λdify)∬−∞∞P(ξ,η)dξdηH(f_x,f_y) = \frac{P(\lambda d_i f_x, \lambda d_i f_y)}{\iint_{-\infty}^{\infty}P(\xi, \eta)\mathrm{d}\xi \mathrm{d}\eta}

衍射受限系统的传递函数（OTF）

根据物理意义，其可以通过交叠部分面积来求解其传递函数值（自相关）。

例1：衍射受限的非相干OTF的计算

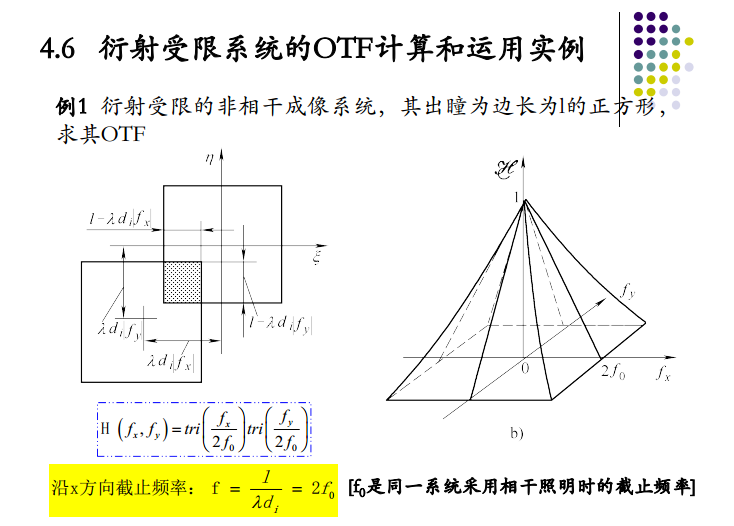
衍射受限的非相干照明情形，其截止频率是相干照明情形下截止频率的两倍。

五、 像差对成像系统传递函数的影响

既影响对比度（振幅），也会影响相位传递。

5.1 广义光瞳函数

系统像差效应集中表现为：

出瞳面上的波前会偏离理想会聚球面波的像面。
以波像差 w(x,y)w(x,y) 描述该像差（光程差），像差产生的位相差：

ejkW(x,y)e^{jkW(x,y)}

广义光瞳函数：

P(x,y)=ejkW(x,y)P(x,y)P(x,y)=e^{jkW(x,y)}P(x,y)

离焦系统OTF

不需要计算，只需要了解分析的过程，知道离焦像差会带来何种影响。

非相干照明，存在固定分辨极限。

相干照明，不存在固定分辨极限，分辨率随着位相而改变。

𝑓_𝑥=𝑥_2/ ×∬_(⤶23−∞)^∞▒〖𝑈_1^′ (𝑥_1,𝑦_1 ) 𝑒^(𝑗𝑘/(2𝑓_1 ) (𝑥_1^2+𝑦_1^2 ) ) 〗 𝑒^(−𝑗𝑘/(𝜆𝑓_1 ) (𝑥_1 𝑥_2+𝑦_1^ 𝑦_2 ) ) ⅆ𝑥_1 ⅆ𝑦_1 𝑈_2=𝑗𝑘𝑓_1∙𝑒^(𝑗𝑘𝑓_1 )∙𝑒^(𝑗𝑘/(2𝑓_1 ) (𝑥_2^2+𝑦_2^2 ) )

第七章 全息投影

7.4 制作全息光栅

思路：

  1. 先写出两种光波
  2. 写出在记录平面上的，两光束的振幅叠加振幅 -> 双光束干涉。
  3. 求得平面光强（包含频率）
  4. 得到频率项（展开）

I(x,y)=2+2cos[2πx2sin(θ/2)λ]I(x,y) = 2 + 2 \cos \left[ 2 \pi x \frac{2\sin (\theta/2)}{\lambda} \right]

  • 记录结果：记录介质透过率函数 与 相干光强 成正比 -> 记录下相干条纹。
  • 空间频率：把已知参数代入，求得：

f=2sin(θ/2)λf = \frac{2\sin(\theta / 2)}{\lambda}

平面波 -> 基元光栅

点光源 -> 基元波带片

把物体看做是很多点源，记录光波为他们在记录介质平面上的相干叠加光波强度。

相关假设：

  • 物光：O(xo,yo,zo)O(x_o,y_o,z_o)
  • 参考光源：R(xr,yr,zr)R(x_r,y_r,z_r)
  • 照明光波：C(x,y)C(x,y)

比较近，满足菲涅尔近似 -> 菲涅尔全息图。

注：

  1. 物光和参考光，通过菲涅尔衍射到达介质平面
  2. 在介质平面上产生相干叠加

I(x,y)=∣R∣2+∣O∣2+Ro+Oo∗ej2πλ[(x−xr)+(y−yr)]I(x,y) = |R|^2 + |O|^2 + R_o+O_o^{*}e^{j\frac{2 \pi}{\lambda}\left[ (x-x_r) + (y-y_r) \right]}

  1. 怎样理解结果？
    结果是：沿着某个方向的平面波，乘上了一个球面波因子，结果是一个与平面波同向的球面波。
  • –> 承载了球面波信息的空间平面波。
  • 相当于一个透镜和棱镜的组合。
  1. zi<0z_i<0 为发散球面波（实像），否则为会聚球面波（虚像）。
  2. 存在放大率问题：
  • 横向放大率：
  • 纵向放大率：z方向比值

几种特殊情形

  1. 再现光波与参考光波完全一样时

xc,=xrx_c,=x_r

  1. x
  2. 当参考光和照明光波为平面波，物体是点光源，则物体与成像得到的位置是关于介质平面对称的。
    可以得到准确位置；

7.5 傅里叶变换全息图

  • 物体和图像的光信息，既表现在它的物体光波中，也蕴含在它的空间频谱内。
  • 用全息方法，可以在空域中记录物光波，也可以在频域记录它的频谱。

假设：

  • 物光： O(x,y)O(x,y)
  • 频谱： G(fx,fy)G(f_x,f_y)

注意：

  • 可以记录：物频谱信息、物频谱的共轭信息
  • 也许共轭信息比物体信息更为重要（光学信息处理）

再现：

  • 平面波入射
  • 需要使用透镜，进行傅里叶变换
  1. 几何光学：放大率分
  • 轴向放大率
  • 垂轴放大率
  • 角放大率
  1. 含有一次位相因子：一个特定方向的平面波
    一次位相因子：
e^{j2a \pi f_x} , e^{j2b \pi f_y}, e^{j2a\pif_x + f_y}
  1. 球面波：没有传播的优先方向。
  2. 球面波的完整性：球面波部分遮挡，其他部分会不会发生改变？
  3. 频谱函数平凡的傅里叶：自相关
  4. ★ 共轭：位相像差为 π\pi
赏